

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | public class Waffle { // Fields private boolean isDelicious; private int numStrawberries; // Constructors public Waffle(boolean isDelicious, int numStrawberries) { this.isDelicious = isDelicious; this.numStrawberries = numStrawberries; } // Methods public boolean isDelicious() { return isDelicious; } public void addStrawberries(int num) { this.numStrawberries += num; } } |
1 2 3 4 5 | public static void main(String[] args) { int numStrawberries = 35; Waffle mattsWaffle = new Waffle(true, numStrawberries); mattsWaffle.addStrawberries(10); } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | public class Food { private boolean isDelicious; public static String shout = "YAAAAAAAS!"; public Food(boolean isDelicious) { this.isDelicious = isDelicious; } public boolean isDelicious() { return isDelicious; } public void consume() { System.out.println("nibble nibble"); } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | public class Waffle extends Food { int numStrawberries; public Waffle(int numStrawberries) { super(true); this.numStrawberries = numStrawberries; } @Override public void consume() { System.out.println("nom nom nom"); } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | // Example 1 Food mmm = new Food(true); mmm.consume(); // Example 2 Waffle mmm = new Waffle(35); mmm.consume(); // Example 3 Waffle mmm = new Food(true); mmm.consume(); // Example 4 Food mmm = new Waffle(35); mmm.consume(); |
1 2 3 4 5 6 7 8 9 10 11 | public int count42Iter() { IntList curr = this; int count = 0; while(curr != null) { if (curr.val == 42) count++; curr = curr.next; } return count; } |
1 2 3 4 5 6 7 8 9 10 11 12 13 | public int count42Recur() { if (next == null) { if (val == 42) return 1; else return 0; } else { if (val == 42) return 1 + next.count42Recur(); else return next.count42Recur(); } } |
1 2 3 4 5 6 7 8 9 10 11 | try { bello(); } catch (NullPointerException e) { System.out.println("Po-ka?"); throw new ArrayIndexOutOfBoundsException(); } catch (Exception e) { System.out.println("Hana, dul, sae!"); } finally { System.out.println("Bee-do Bee-do!"); throw new NoSuchElementException(); } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | public static void main(String[] args) { DisneyRides2 d = new DisneyRides2(); d.add("Space Mountain"); d.add("Splash Mountain"); d.add("Small World"); // METHOD 1: // for loop as we've seen before. for (int i = 0; i < d.size(); i++) { System.out.println(d.get(i)); } // METHOD 2: // Using an iterator to abstract away underlying implementation. Iterator<String> iter = d.iterator(); while(iter.hasNext()) { System.out.println(iter.next()); } // METHOD 3: // Short hand for-each loop that uses iterators behind the scenes. for (String s : d) { System.out.println(s); } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 | import java.util.ArrayList; import java.util.Iterator; public class DisneyRides implements Iterable<String> { /** Fields **/ // ArrayList of Objects. Requires cast in get() method. // private ArrayList rides = new ArrayList(); // ArrayList of Strings. Generics eliminates need to cast by specifying static type of contained items. private ArrayList<String> rides = new ArrayList<String>(); /** Methods **/ // Add an item to our list after putting it in all-caps. void add(String ride) { rides.add(ride.toUpperCase()); } // Retrieves item at index i. String get(int i) { // return (String)rides.get(i); return rides.get(i); } // Retrieves number of total items. int size() { return rides.size(); } @Override // Provides a new iterator that starts from beginning of list. public Iterator<String> iterator() { return new DisneyRidesIterator(); } /** Nested subclass to define the iterator for our data structure. **/ class DisneyRidesIterator implements Iterator<String> { // Counter for our iterator. private int i = 0; @Override // Tells us if there are still more items. // Cannot modify current state of data structure in any way. public boolean hasNext() { return i < rides.size(); } @Override // Retrieves next item. // Updates state of data structure for next time. public String next() { String result = rides.get(i); i++; return result; } } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | List<Integer> l = new ArrayList<>(); for (int i = 0; i <= 30; i++) { l.add(i); } l = l.stream() .filter(o -> o%2==0) .collect(Collectors.toList()); int a = l.stream() .map(o -> o*o) .reduce((o1, o2) -> o1+o2) .orElse(0); |
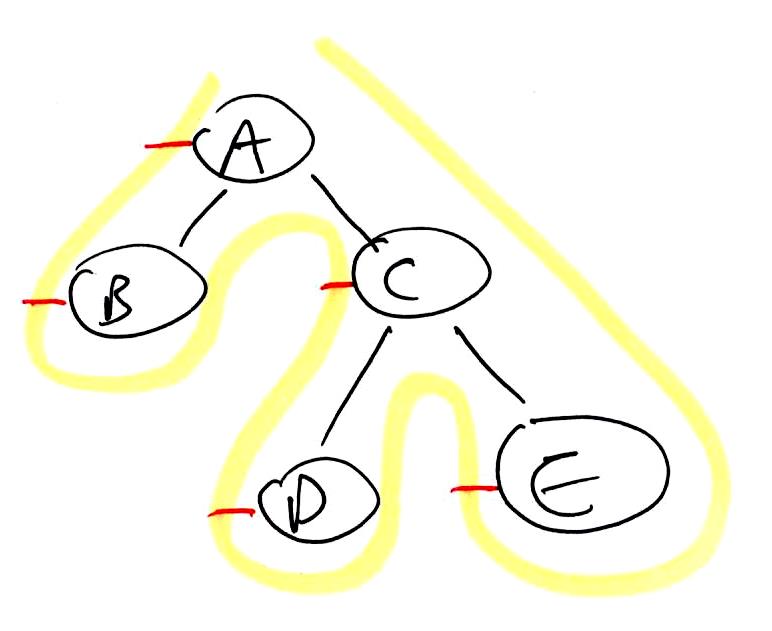
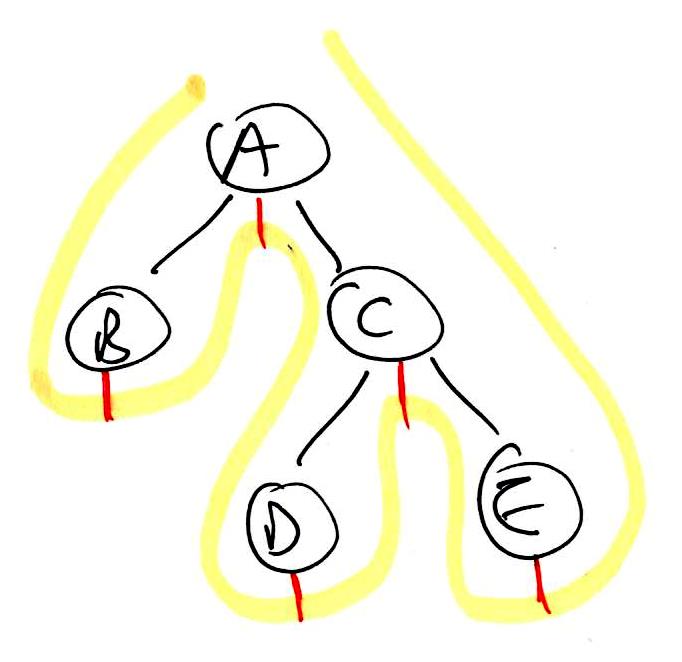
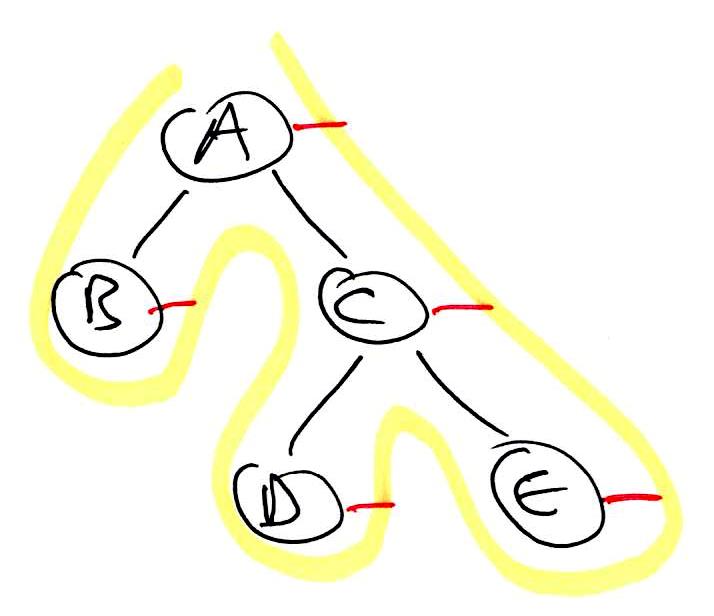
1 2 3 4 5 6 7 8 | binaryTreeTraversal(node):
preorder(node)
if left != null:
binaryTreeTraversal(left)
inorder(node)
if right != null:
binaryTreeTraversal(right)
postorder(node)
|
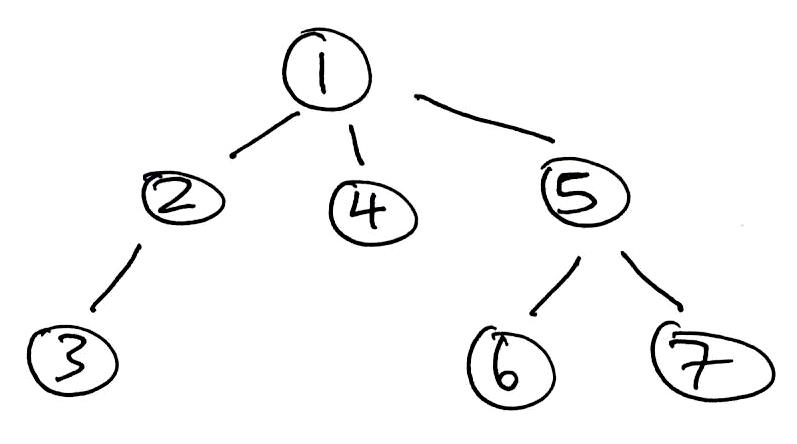
1 2 3 4 5 6 7 | Use STACK as fringe. Add root to fringe. while fringe not empty: Remove next from fringe. Add its children to fringe. Process removed node. |
1 2 3 4 5 6 7 | Use QUEUE as fringe. Add root to fringe. while fringe not empty: Remove next from fringe. Add its children to fringe. Process removed node. |
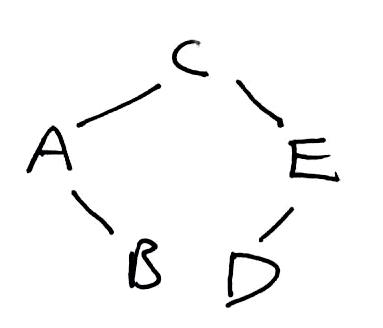
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | public BinaryTree(ArrayList<T> pre, ArrayList<T> in) { root = listHelper(pre, in); } private TreeNode listHelper(ArrayList<T> pre, ArrayList<T> in) { if (pre.isEmpty()) return null; TreeNode subtreeRoot = new TreeNode(pre.get(0)); int rootIndex = in.indexOf(pre.get(0)); subtreeRoot.left = listHelper( new ArrayList<>(pre.subList(1, rootIndex + 1)), new ArrayList<>(in.subList(0, rootIndex)) ); subtreeRoot.right = listHelper( new ArrayList<>(pre.subList(rootIndex + 1, pre.size())), new ArrayList<>(in.subList(rootIndex + 1, in.size())) ); return subtreeRoot; } |
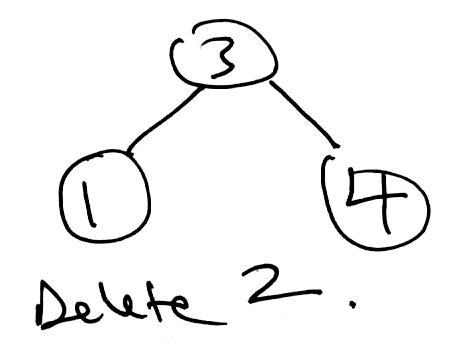
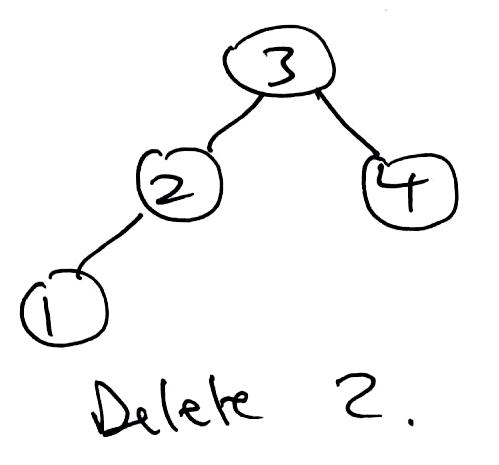
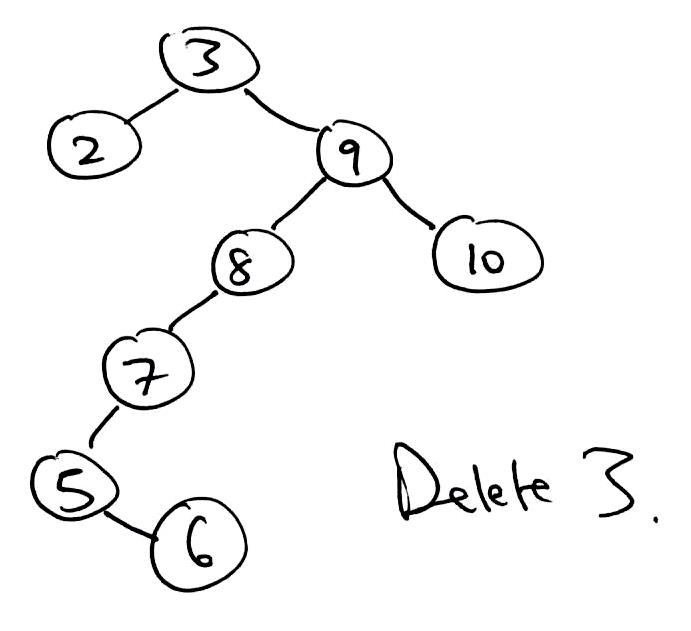
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 | public T delete(T key) { TreeNode parent = null; TreeNode curr = root; TreeNode delNode = null; TreeNode replacement = null; boolean rightSide = false; // Find node to be removed. while (curr != null && !curr.item.equals(key)) { if (((Comparable<T>) curr.item).compareTo(key) > 0) { parent = curr; curr = curr.left; rightSide = false; } else { parent = curr; curr = curr.right; rightSide = true; } } delNode = curr; // Target was not found. if (curr == null) { return null; } // Only has a left child. Remove target and let this take its place. if (delNode.right == null) { if (root == delNode) { root = root.left; } else { if (rightSide) { parent.right = delNode.left; } else { parent.left = delNode.left; } } // Either has two children or just a right child. } else { curr = delNode.right; replacement = curr.left; // There was only a right child. Remove target and let this take its place. if (replacement == null) { replacement = curr; // There were two children. } else { // Find inorder successor replacement. // Leftmost node of target's right child. while (replacement.left != null) { // curr is the parent of replacement. curr = replacement; replacement = replacement.left; } // replacement does not have a left child. // remove replacement by letting its right child take its place. curr.left = replacement.right; // replacement takes delNode's place. replacement.right = delNode.right; } // replacement takes delNode's place. replacement.left = delNode.left; if (root == delNode) { root = replacement; } else { if (rightSide) { parent.right = replacement; } else { parent.left = replacement; } } } // return value of delNode. return delNode.item; } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | public T getKthValue(int k) { return getKthValueHelper(k, root); } private T getKthValueHelper(int k, TreeNode node) { if (node == null) return null; if (k >= node.size || k < 0) throw new IndexOutOfBoundsException(); int numOnLeft; if (node.left != null) numOnLeft = node.left.size; else numOnLeft = 0; if (k < numOnLeft) { return getKthValueHelper(k, node.left); } else if (k == numOnLeft) { return node.item; } else { return getKthValueHelper(k - 1 - numOnLeft, node.right); } } |
1 2 3 4 5 6 7 8 9 10 11 | Use STACK as fringe. Maintain SET of visited vertices. Add start vertex to fringe. while fringe not empty: Remove next from fringe. if not visited: Process removed node. for each neighbor: Add to fringe. Mark removed node as visited. |
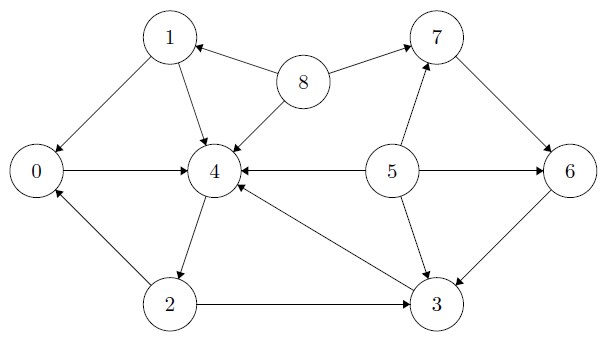
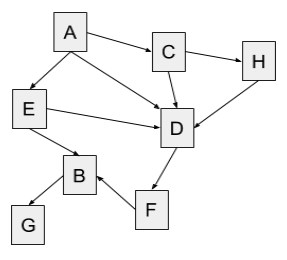
1 2 3 4 5 6 7 8 9 10 | Maintain a FRINGE. Maintain ARRAY of current in-degrees of all vertices. Add in-degree 0 vertices to fringe. while fringe not empty: Remove next from fringe. Process removed node. for each neighbor: Decrement its current in-degree. Add to fringe all new in-degree 0 vertices. |
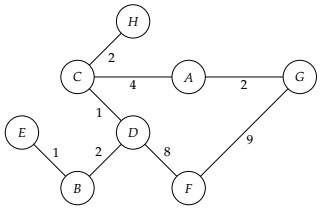
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | Use PRIORITY QUEUE as fringe. Maintain SET of visited vertices. Remember shortest paths to each vertex found so far. Add start vertex to fringe. while fringe not empty: Remove next from fringe. Mark as visited. The shortest path to the removed vertex has now been finalized. for each neighbor: if not visited && (shortest path to removed vertex + distance from removed vertex to neighbor) < current shortest path to neighbor: Either add to fringe or if already in fringe, update current shortest path to neighbor. |
1 2 3 4 5 | <body> <h1>Oolong</h1> <a href=”www.earl-gray.io”>50% sugar, less ice</a> <center><b>Pumpkin Spice Latté</b></center> </body> |